Este tutorial muestra el uso del programa OR Brainware Decision Tools para resolver problemas de planeamiento de la producción en donde las variables de decisión tienen requerimientos de ser variables enteras o binarias.
Considere el siguiente caso:

Fuente: Moya. Investigación de Operaciones.
A continuación se mostrará el uso del programa OR Brainware Decision Tools para resolver el caso:
Paso # 1: Ejecutar OR Brainware Decision Tools.
Paso # 2: Seleccionar el módulo de «Modelado Con Programación Lineal».
El problema tiene 6 variables de decisión y 7 restricciones funcionales. Sean XA , XB y XC la cantidad de casas modelo A, B y C que deben fabricarse. YA, YB y YC serán las variables de decisión que indicarán si el equipo se alquila o no. En este caso XA , XB y XC son variables que tomarán valores enteros, y YA, YB y YC serán variables que tomarán valores binarios 0/1. El uno indica que el equipo debe alquilarse, y el cero indica que el equipo no debe alquilarse.
El modelo a resolver es el siguiente:

Seleccionar el botón «Crear Modelo» e indicar que el número de variables de decisión es seis (6) y el número de restricciones es siete (7). Luego seleccione el botón Ejecutar. Este paso creará la estructura del modelo de programación lineal, por lo que el usuario solo tendrá que cambiar el nombre de las variables si lo desea e introducir los datos correspondientes.
Paso # 3: Introducir los respectivos coeficientes tecnológicos de las restricciones, los coeficientes de costo de la función objetivo, así como los lados derechos de las restricciones y sus respectivos operadores aritméticos “Mayor Que”, “Menor Que”, ò “Igual a». Resuelva el problema presionando el botón “Menú” y seleccionando la opción “Resolver Programa Lineal Entero Mixto” para un problema de «Maximizar». Aparece la siguiente pantalla:
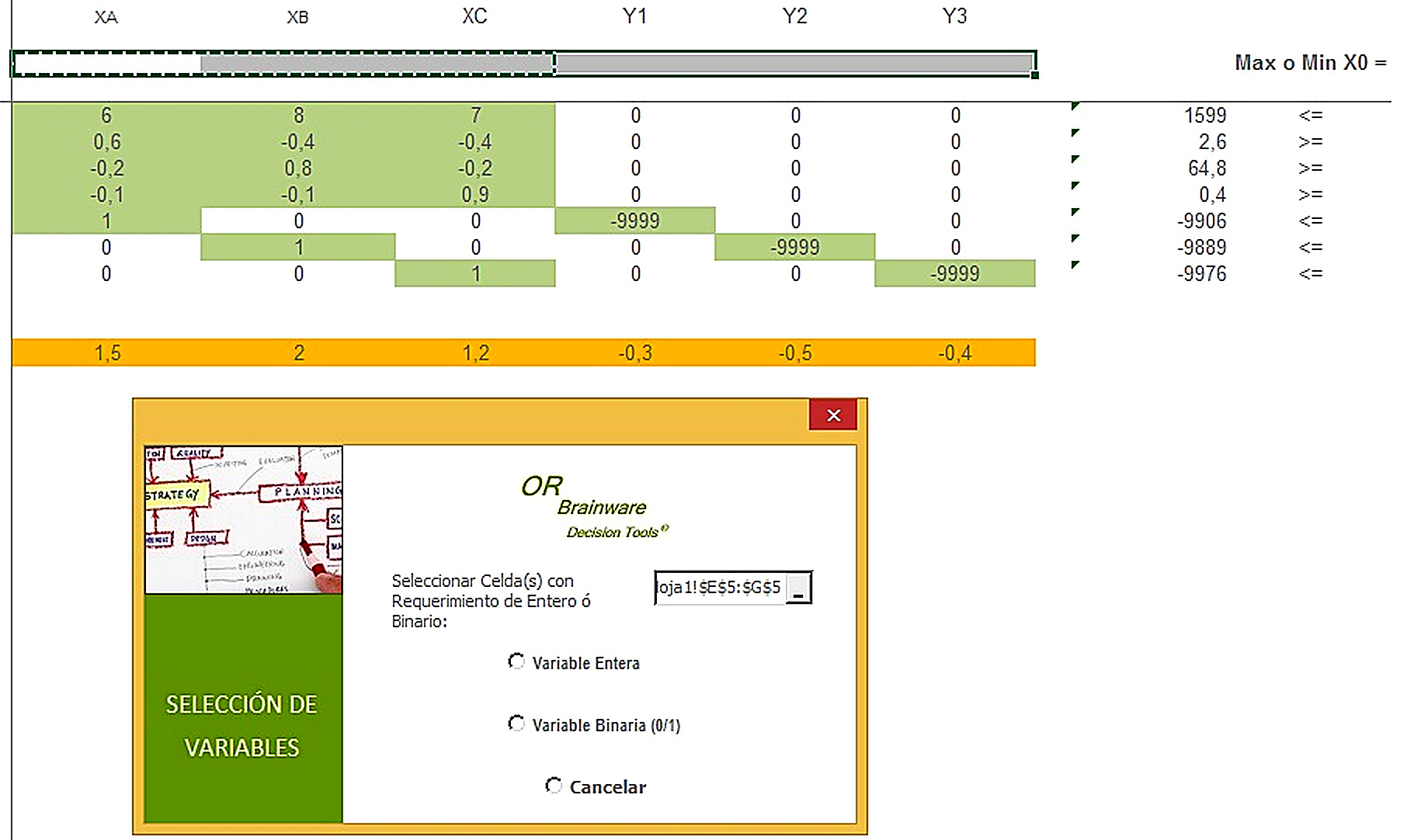
A continuación se selecciona el rango de las variables XA, XB Y XC y se marcan como variables enteras en el botón correspondiente. A la pregunta de si se seleccionan más variables, se selecciona la opción «Si» y luego se marcan las variables Y1, Y2 y Y3 como binarias. Al resolver se muestra la siguiente pantalla con la solución.
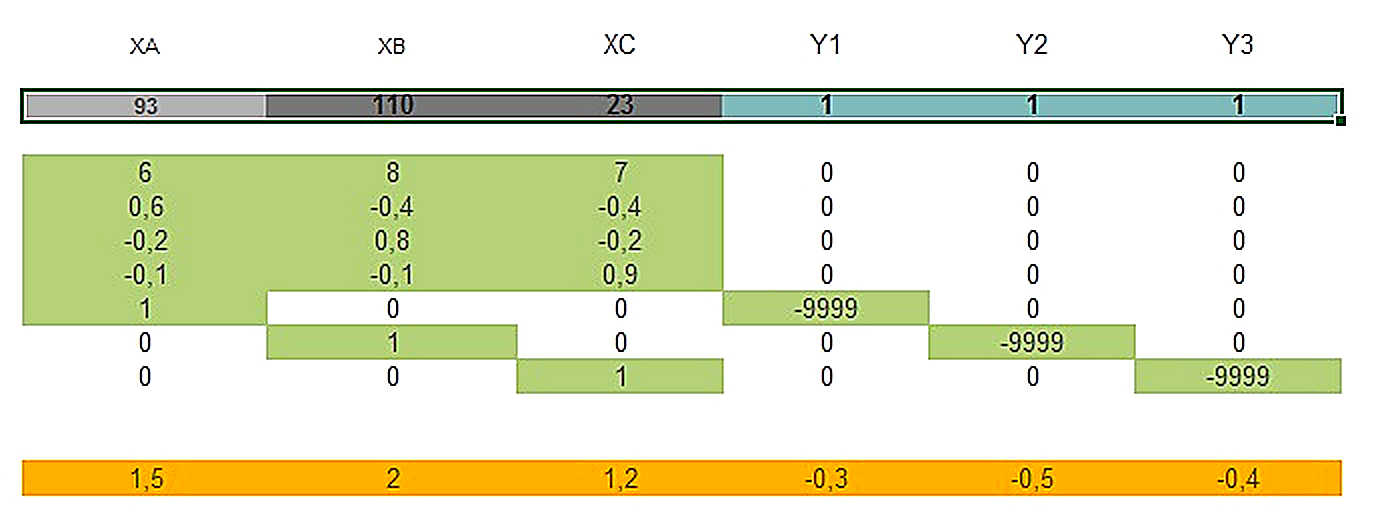
Las celdas pintadas de color gris son las variables con requerimientos de solución entera, y las pintadas de celeste son las que tienen requerimientos de variables binarias.
Paso # 4: Si se desea, se puede generar el informe de resultados, como se muestra a continuación.
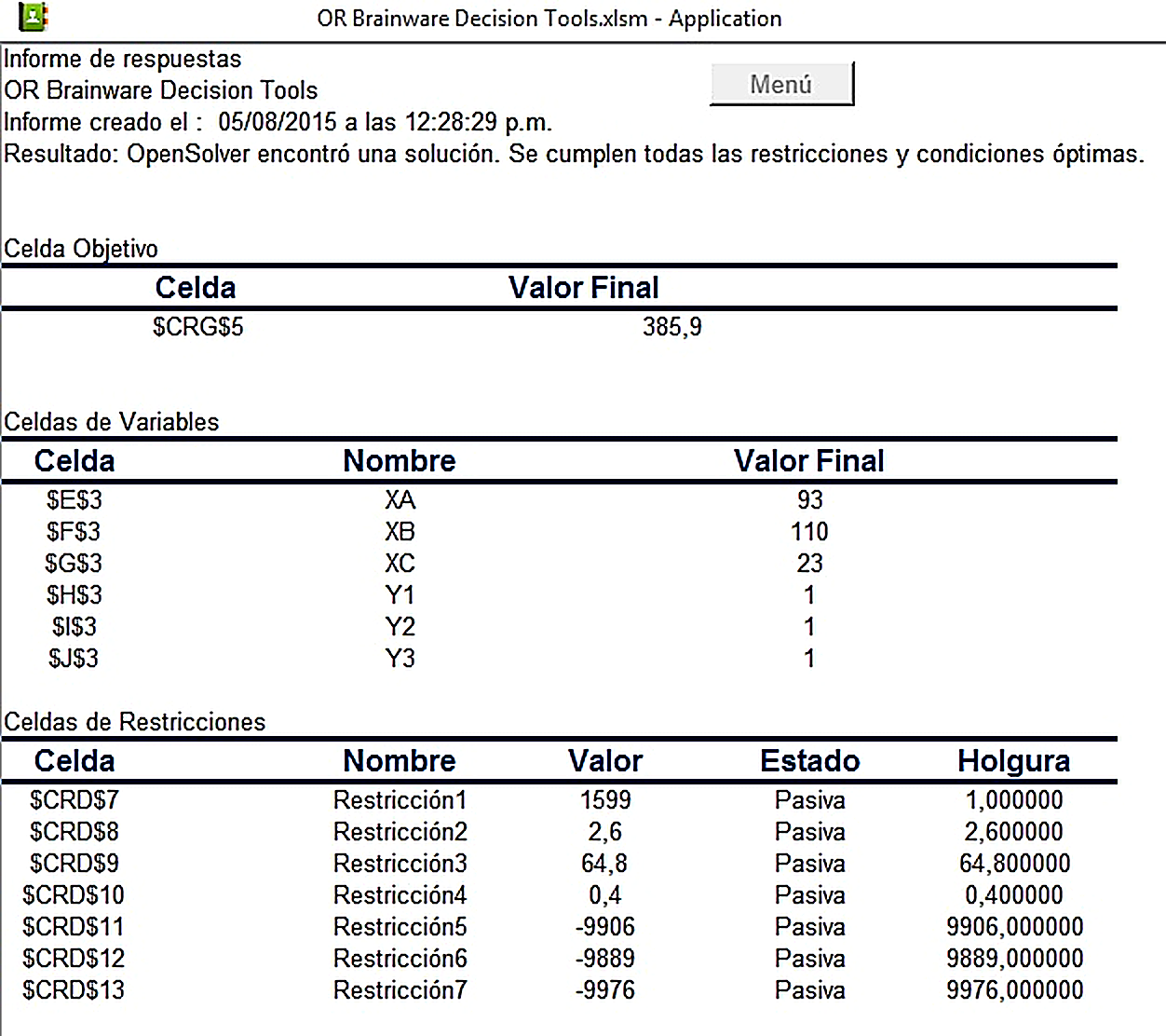
La solución óptima del modelo indica que deben producirse 93 casas modelo A, 110 casas modelo B y 23 casas modelo C para una ganancia máxima de 385.9 millones de unidades monetarias.